OpenAI研究员首次提出「AGI时间」进化论！o1数学已达「分钟级AGI

本月，OpenAI科学家就当前LLM的scaling方法论能否实现AGI话题展开深入辩论，认为将来AI至少与人类平分秋色；LLM scaling目前的问题可以通过后训练、强化学习、合成数据、智能体协作等方法得到解决；按现在的趋势估计，明年LLM就能赢得IMO金牌。

随着AI不断刷新各项基准测试，关于AI的发展各方也态度不一。

早在本月5日，「泛化的未知未来」研讨会上，众多知名研究员就相关话题展开了一场针锋相对的辩论。

此次辩题是 「当今的LLM沿着既有路线持续发展是否就足以实现真正的AGI」。

辩论分为两个阵营：「火花派」认为现有技术已经具备或即将具备解决这些难题的能力；「余烬派」则持怀疑态度，认为需要更多质的变化。

正方辩手Sébastien Bubeck

辩论正方是Sébastien Bubeck，在辩论五周前加入OpenAI，是「Sparks of Artificial General Intelligence」的第一作者。

论文地址：https://arxiv.org/pdf/2303.12712

在过去几年里，Sébastien Bubek由于专注于研究大模型的智能涌现问题，所以更加主张随着大模型的智能涌现，就足以产生解决现存NP难题以及黎曼假设的智能水平。

反方辩手Tom McCoy

反方是Tom McCoy，目前是耶鲁大学语言学助理教授，是「Embers of Autoregression」一文的第一作者。

论文地址：https://arxiv.org/pdf/2309.13638

他在约翰霍普金斯大学获得认知科学博士学位，并在普林斯顿大学作过计算机科学的博士后， 博士后导师是Thomas Griffiths。

今年他开始在耶鲁大学担任语言学助理教授，从事计算语言学、认知科学和人工智能的研究。他对人和机器如何学习以及表示语言结构感兴趣。

现有的LLM能够基于扩展解决重大数学问题吗？

Sébastien表示过去几年LLM取得的进步「简直是奇迹」。

重大未决数学猜想是指那些大多数人类专家认为无法用当前证明技术解决的问题，比如P≠NP或黎曼猜想。

比如，在MMLU基准中，最佳模型已超过了90%，已经彻底饱和。在医疗诊断领域，GPT-4则达到了90%正确率，而人类医生才达到了75%准确率。

并且与辩题相关的高中数学竞赛基准很快也会饱和。

Google最新发布的AI数学家，通过微调的Gemini系统，可以拿到2024年国际数学奥林匹克竞赛银牌。

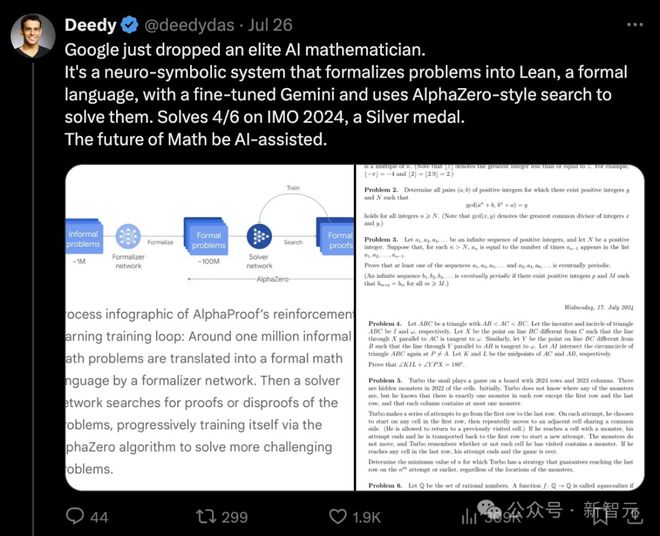
基于这种趋势， Sébastien认为到明年LLM拿下IMO的金牌不是问题。

随着各种基准日益饱和，Sébastien表示真正衡量AI进步的尺度应该是「AGI时间」。

Sébastien：扩展AGI时间足以解决

GPT-4目前处于「秒级AGI」，在许多情况下可以快速响应并给出答案，类似于人类可以极短时间内作出反应。

对于某些编程任务，GPT-4可能已经达到了「分钟级AGI」，即它能像人类一样花几分钟时间编写代码片段。

而o1则可能已经达到了「小时级AGI」。

在数学领域，GPT-4仍然停留在AGI秒阶段，即便是o1也只是「分钟级AGI」，因为它无法像人类那样花费较长时间深入思考复杂的数学问题。

Sébastien表示对于重大开放性问题的解决，类似于黎曼猜想等重大数学问题的证明，那就可能需要AGI能够持续深入研究问题并坚持数周。

他表示道：「如果你有『周级AGI』的能力，那么你就拥有了这一切。」

Tom：依然欠缺创造性飞跃

而Tom则对Sébastien的观点抱以怀疑的态度，他认为仅靠现有方法的扩展是不足以去解决复杂的数学猜想的。

Tom McCoy的核心观点是证明数学猜想需要某种创造性的飞跃。

「很可能我们还欠缺某种创造性的飞跃，也就是一种全新的证明思路。在有了这种新思路之后，还需要结合长时间的推理与规划，最后才能形成符合学术标准的可信且完整的证明」。

他表示虽然LLM不仅仅是记忆，但是其泛化能力并不足以解决数学猜想，因为解决数学猜想「需要提出一个全新的想法，而不仅仅是已有想法的组合。」

而且他认为LLM缺乏长期推理和规划的能力，它们的能力很大程度上取决于训练数据的性质。这也是他们「Embers of Autoregression」论文的主要观点。

而且至关重要的是，到目前为止的扩展（scaling），并没有从根本上解决这个问题。

「我们需要的是根本性的变革，因为对于新的证明方法来讲，其在训练数据中的频率是0。所以无论怎么去继续扩展规模，都不会让LLM能够接触到这些新的证明方法，至于继续从这些新的方法里继续学习也就无从谈起了」。

Tom还表示由于LLM幻觉的存在，让其形成洋洋洒洒数十页乃至数百页的可信数学证明是不现实的。

「问题在于，当需要撰写的证明很长时，即使我们能大幅降低幻觉出现的概率，但只要这个概率不为零，当证明足够长时，证明中出现错误的可能性就几乎是必然的。而且只要证明中存在一处缺陷，这个证明就无效了」。

所以Tom认为，为了给出可信的严谨证明，LLM需要的是质变，而不仅仅是扩大规模所带来的那种量变收益。

总的来说，Tom认为有两个关键因素阻碍了当前LLM方法实现解决重大数学猜想。

第一是需要实现创造性的飞跃，产生全新性质的想法。第二是能够在数十页或数百页的篇幅中进行持续的长期推理和规划。

结合与扩展推理

Sébastien：「组合」就足以强大

为了反驳Tom的「模型的泛化能力仅仅是将两个不同的想法组合」，Sébastien询问在坐的听众：「你觉得你做的比仅仅将现有的想法结合起来更多吗？」

Sébastien认为将事物互相结合的这个过程本身就附带了一定的随机性，类似于在「思维空间里随机游走」。不断地组合现存事物，即可产生突破性的成果。

「至少对我来说，当我回顾自己所做的事时，我觉得大部分都是在做组合的工作，然后添加一点随机性进去。实际上，我写过很多论文，在其中我借鉴了别人的成果，然后意识到他们所做的其实也只是在组合已有的东西。」

错误也可以在多智能体环境被纠正

Tom的第二个核心论点是「随着推理变得越来越长，错误是不可避免」。

对此，Sébastien认为问题被夸大了。即便是知名研究员撰写的论文，如果它们超过了50页还能保持完全正确的，也是非常非常少。

但这不意味着论文的结果是错误的，况且错误也可以被他人所指正。

「我可以想象一个未来，有一群AI共同工作。那将是一个多智能体的环境，其中一些AI在阅读其他AI写的论文，然后指出错误并得到修正回馈，等等。这绝对是一个可能的未来」。

后训练是否可以解决现存问题

Sébastien对于「Embers of Autoregression」一文中提到的问题，即训练数据表示不充分时会出现更多错误。

「当然，这绝对是一个真实的陈述，但它只是针对基础模型的真实陈述。」

但是Sébastien认为这并不意味着模型本身就不具备能力，只是因为训练数据中一些任务表示不够充分。所以可以通过后训练来提取相应的能力。

他对Tom讲道：「我认为你在Embers of Autoregression论文中提到的只是关于基础模型的内容。如果你对其进行后训练，一些结论可能会改变。」